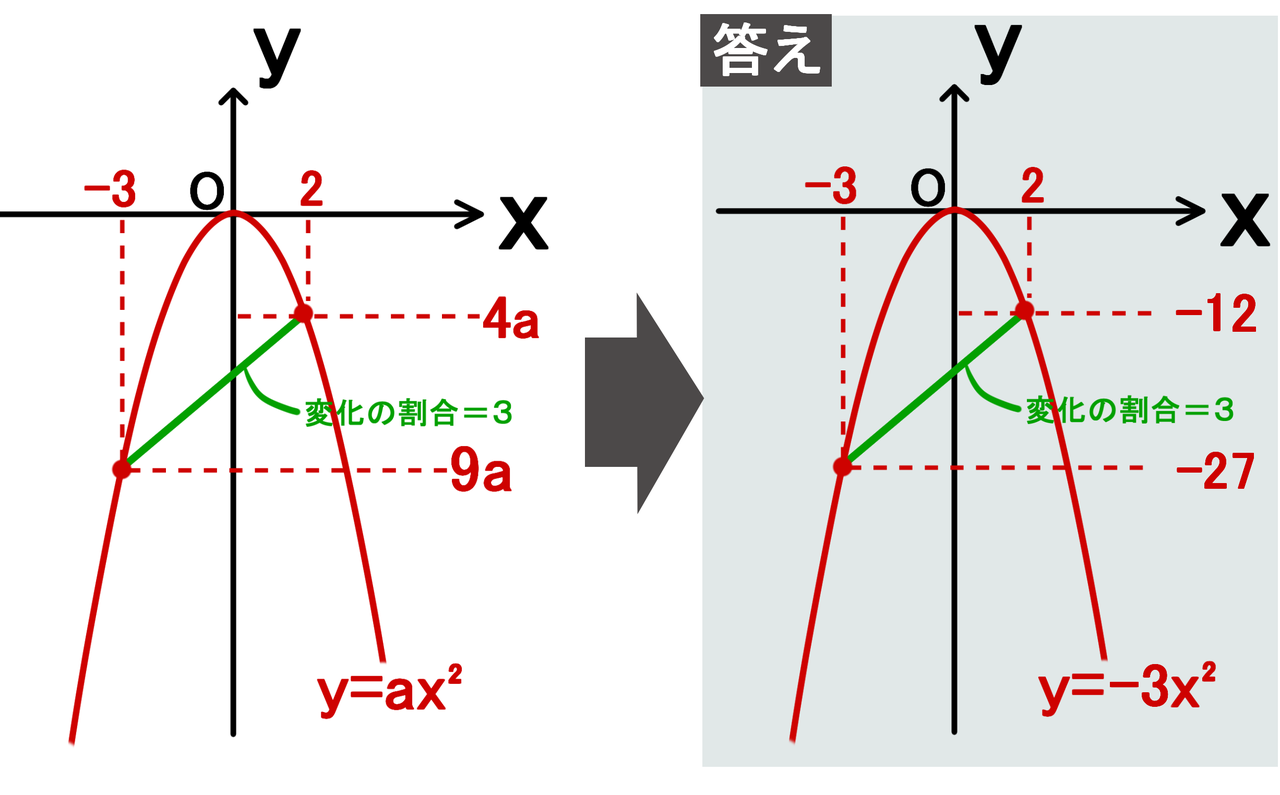
基本 二次関数y A X P 2のグラフ なかけんの数学ノート
ここでは、二次関数のグラフを見ながら ・解の存在範囲（どこでx軸と交わっているか）や ・y=ax 2 bxcで表されたの (a,b,c)などの符号（正負）を判定する問題 を解く際に着目すべきポイントをまとめました。 前半は「2次関数の基本」を解説しているのでまた、グラフは永遠に下方向に伸びていくので最小値はありません。 上の2問のようにグラフに定義域が与えられていないときは、 グラフが最大値、最小値を持たない場合もある ので注意して下さい。 定
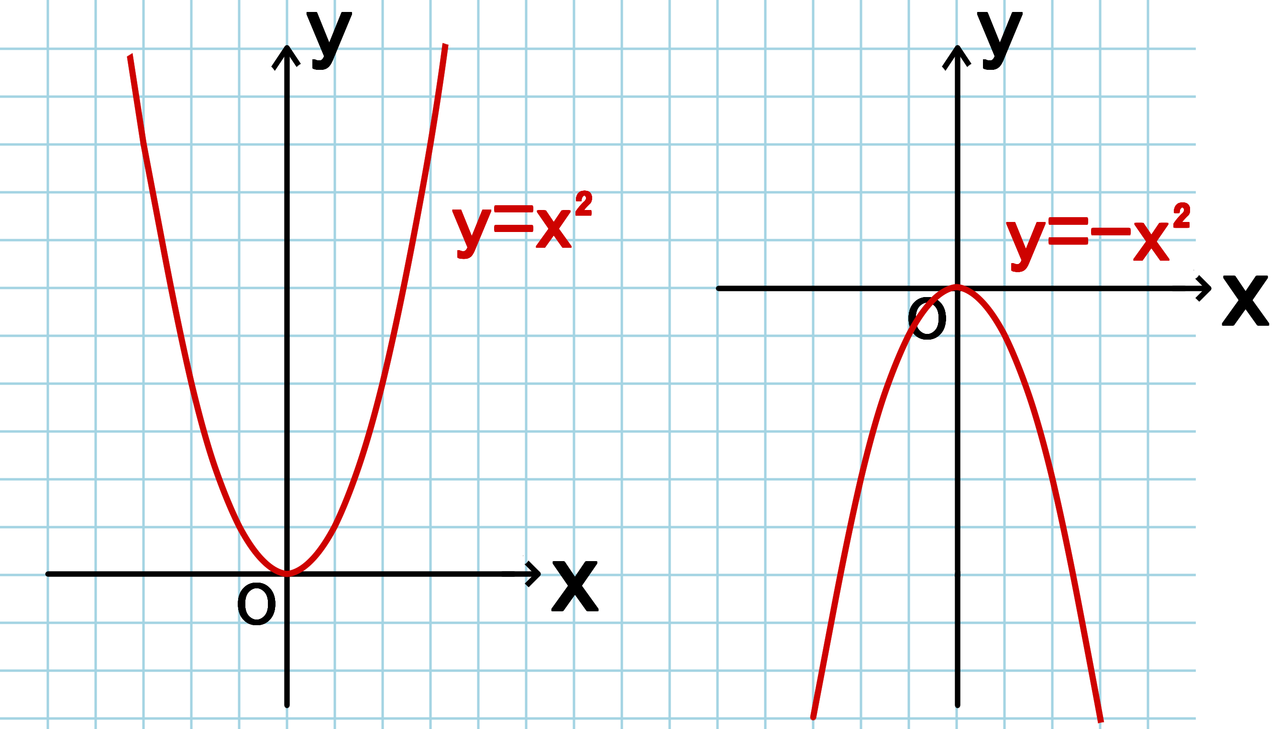
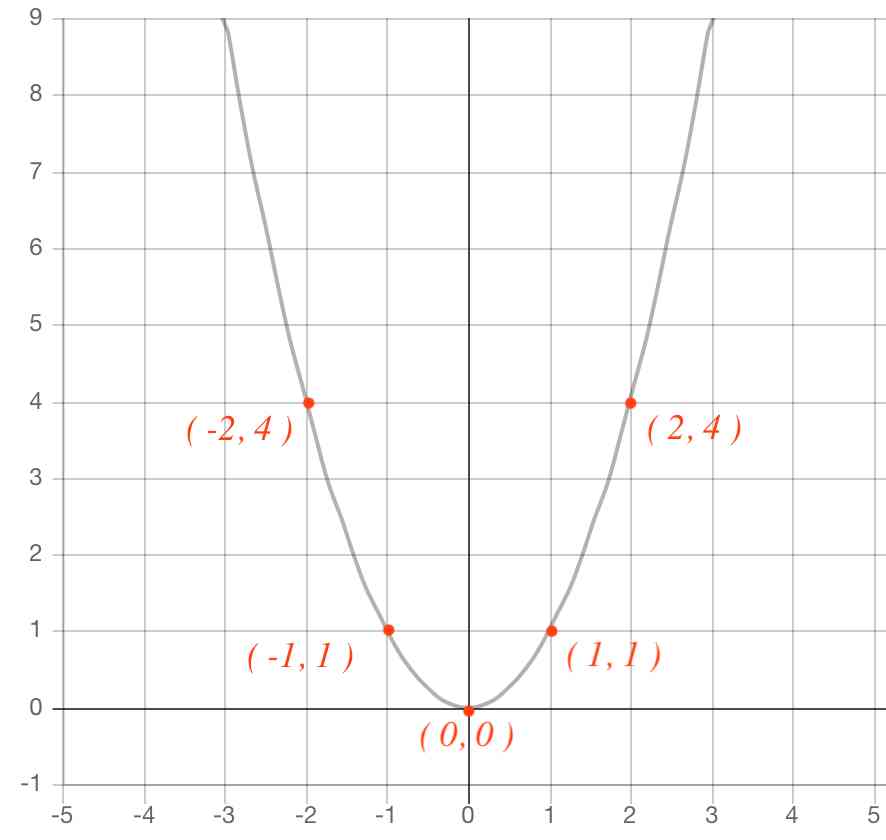
二次関数 y=x2乗 グラフ
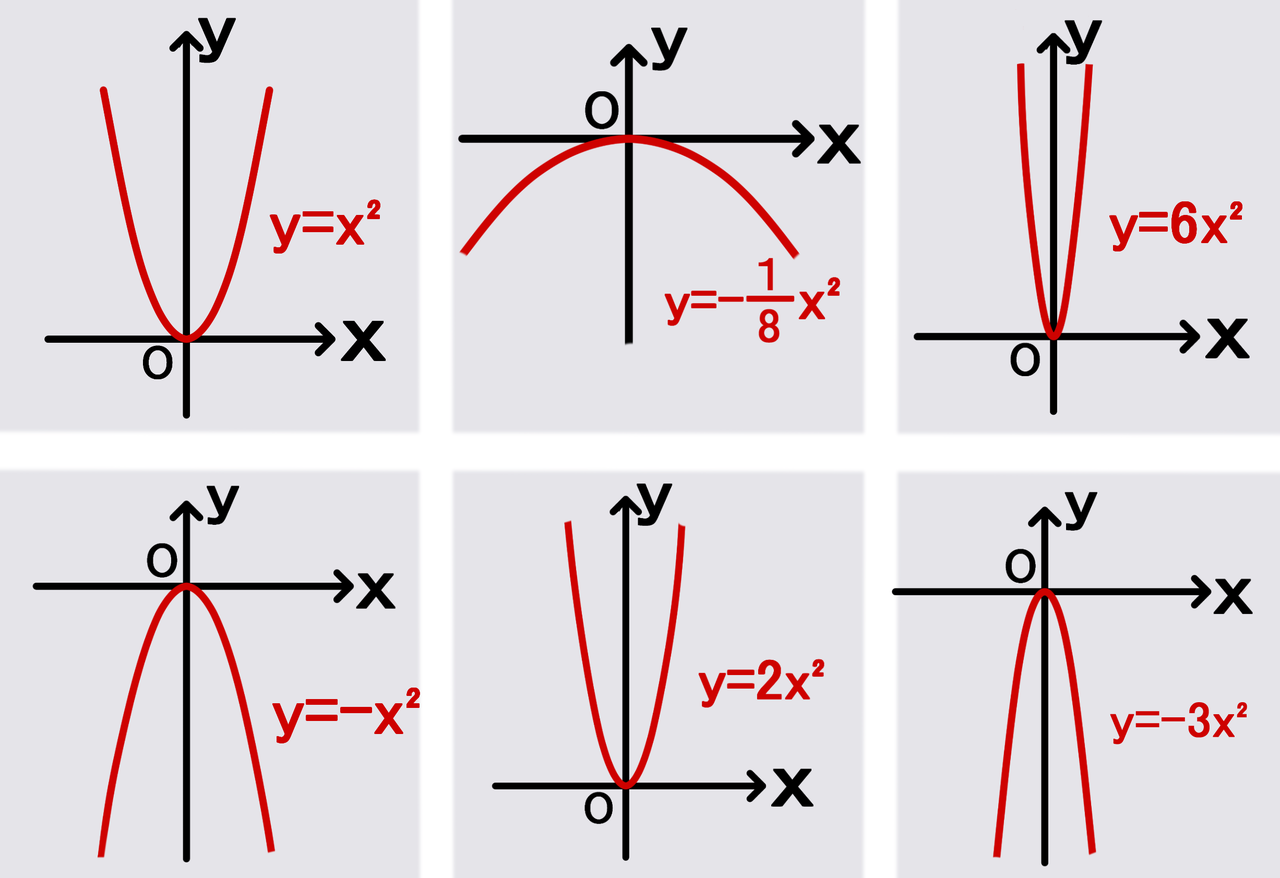
二次関数 y=x2乗 グラフ-次に、先ほとの基本の二次関数 y = x 2 を発展させて、 y = ax 2 のグラフについて考えてみましょう。 この変数 a は、二次関数のグラフの尖り具合を表しています。 先ほどの基本形では、 a = 1 の時について考えていたことになりますね。 では、この係数 a aを変化させるとどのようにグラフの形状 続いて、二次関数のグラフを書いていきましょう。 二次関数のグラフも、多くの生徒から嫌われています。 それは二次関数のグラフの形が「変な曲線」であり「上から下へ、下から上へと動く」からです。 一次関数のグラフはとても単純でした。
２次関数 ２次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん
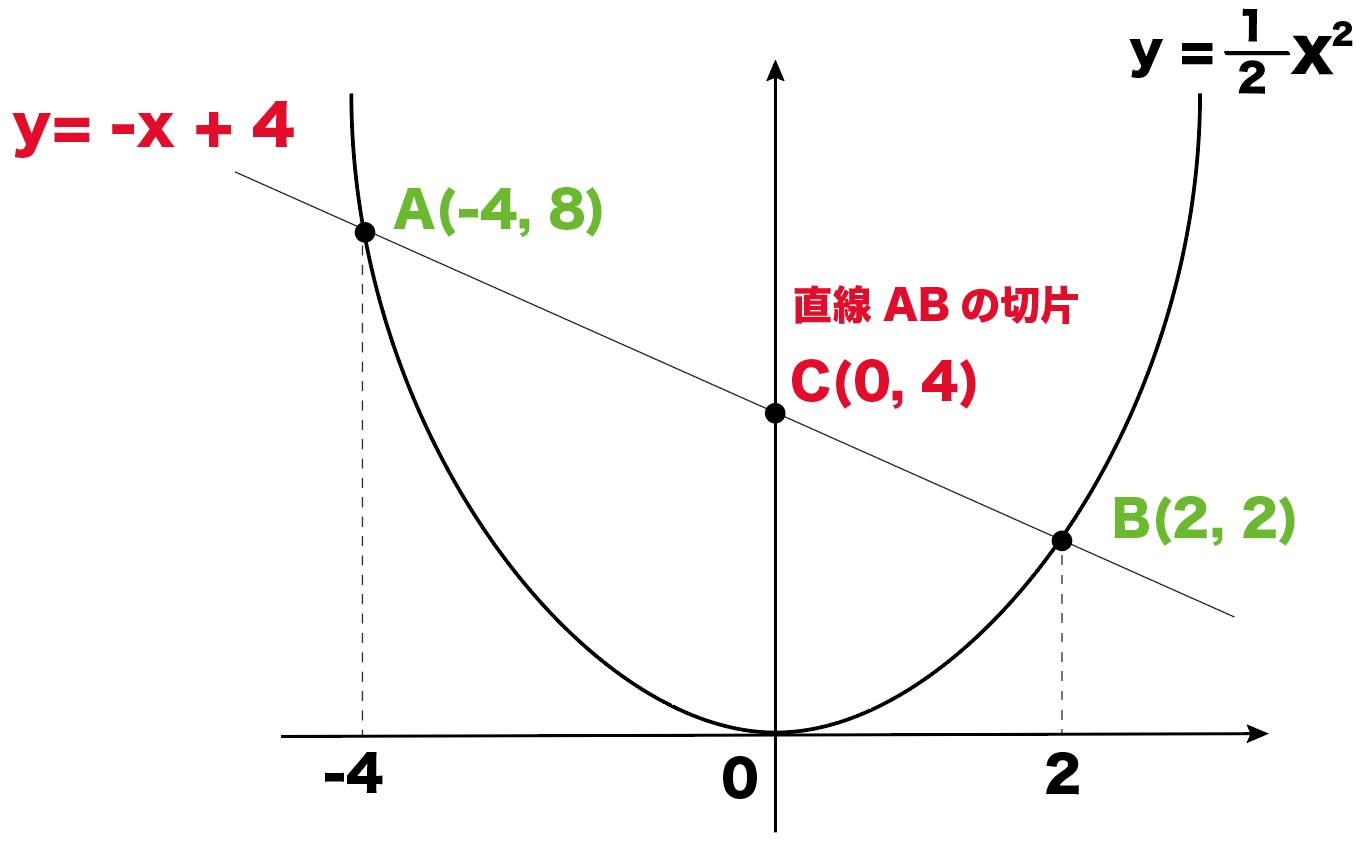
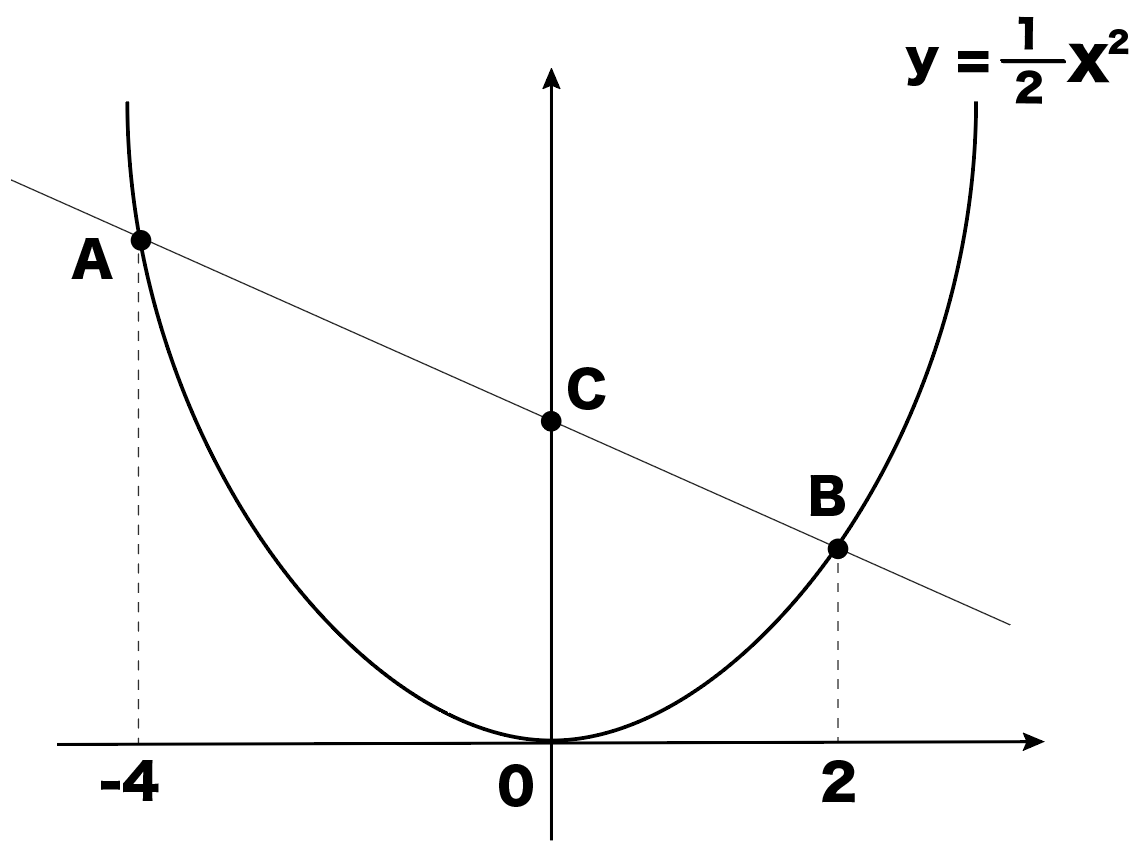
右図のように2次関数 y=x 2 のグラフと直線 y=x2 のグラフが x 軸， y 軸と交わる点をそれぞれ D ， C とするとき，次の問いに答えなさい． (1) 点 C ， D の座標を求めなさい． (2) 点 P は2次関数 y=x 2 のグラフ上で x 二次関数のグラフの平行移動とは？公式や応用問題3選をわかりやすく解説 二次関数の最大値・最小値の解き方2つのコツとは？21枚の画像で解説します 二次関数の決定とは？問題の解き方3パターンをわかりやすく解説します 判別式dとは？Y＝ax2乗のグラフ書き方 まとめ お疲れ様でした！ 放物線のグラフを書くためには 丁寧に点を取って、それらをなめらかーに結ぶ！ これだけですね。 何度も練習すれば 誰にでも簡単に書けるようになります。 レッツ！ 練習 (/・ω・)/
二次関数の最大値・最小値の問題 二次関数の最大値・最小値を求める問題では、「 頂点を調べること 」「 グラフを書くこと 」が最大のポイントです。 複雑な条件を考えるときでも、グラフのかたちがイメージできていれば対処できます。X x の変域をすべての数としてグラフにすると， y =x2 y = x 2 のグラフは原点を通り y y 軸について対称な放物線です。 実施時期 3年生2学期（9月） 単元項目 4章1節 関数 y=ax2 y = a x 2 （p104） 配当時数 10時間 指導内容中1です。「比例のグラフ」、かき方のコツは？ 中1です。「比例のグラフ」、比例定数が分数の時は。 中1です。「反比例のグラフ」、かき方のコツは？ 図形の「公式」が覚えられません。 中2です。「連立方程式」のコツを知りたいです！
二次関数 y=x2乗 グラフのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 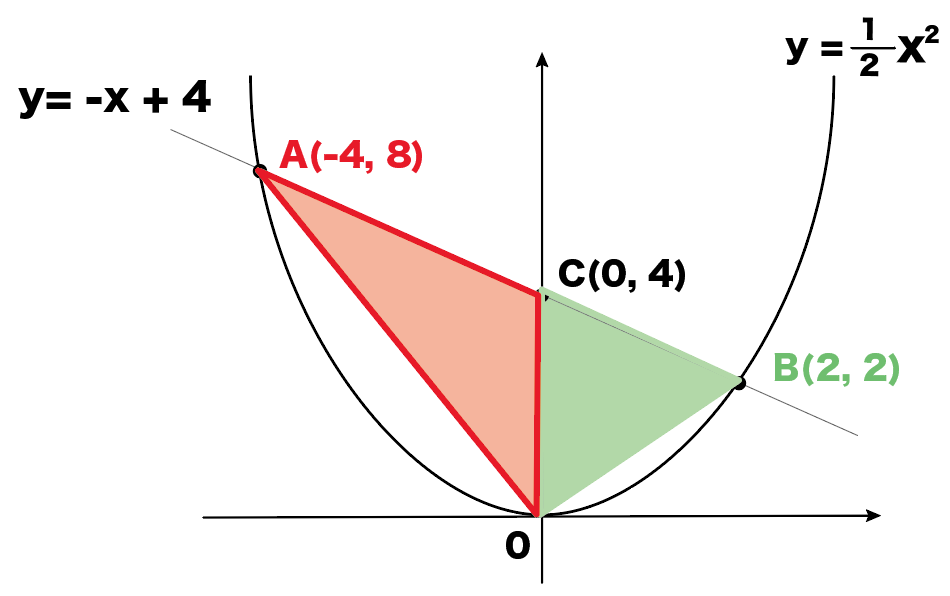 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 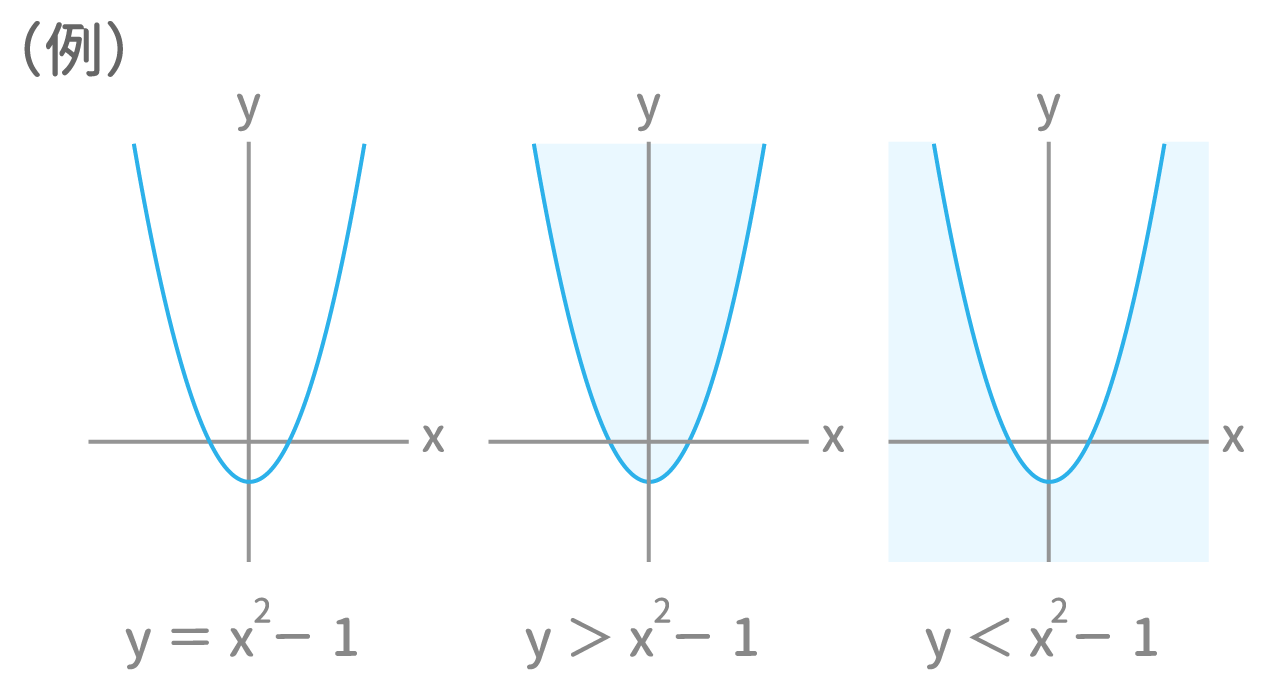 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 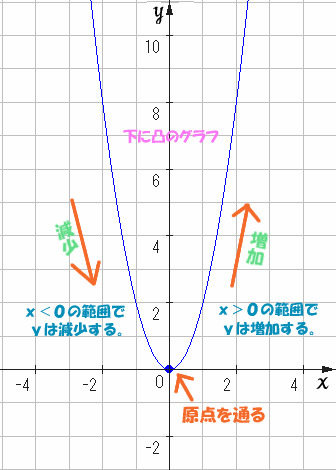 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 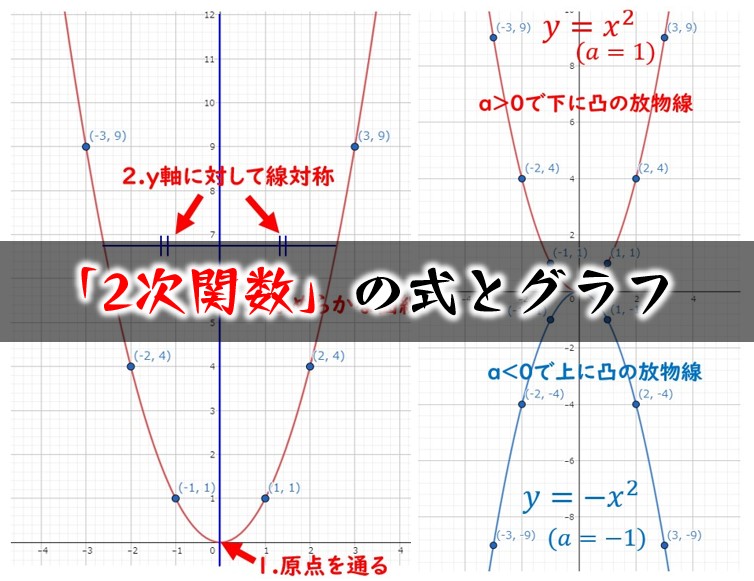 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |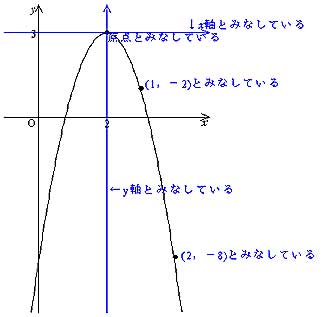
関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 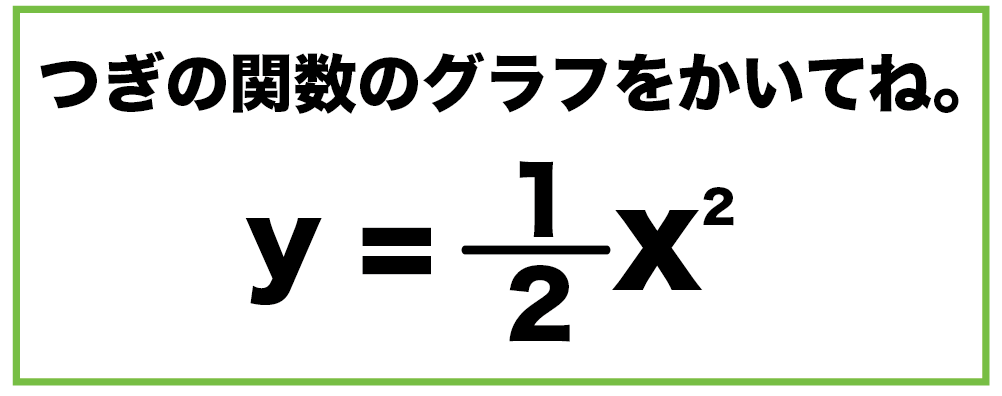 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 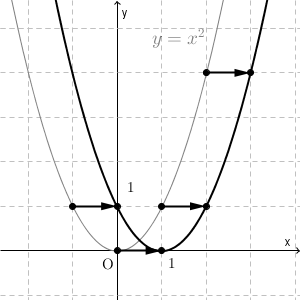 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 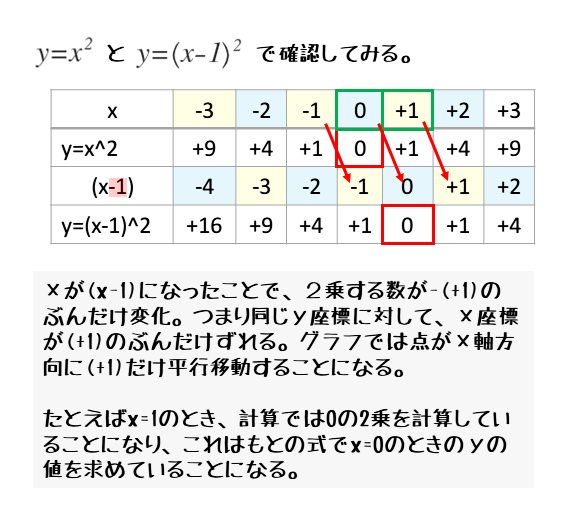 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 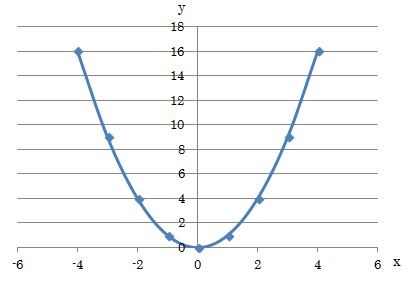 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 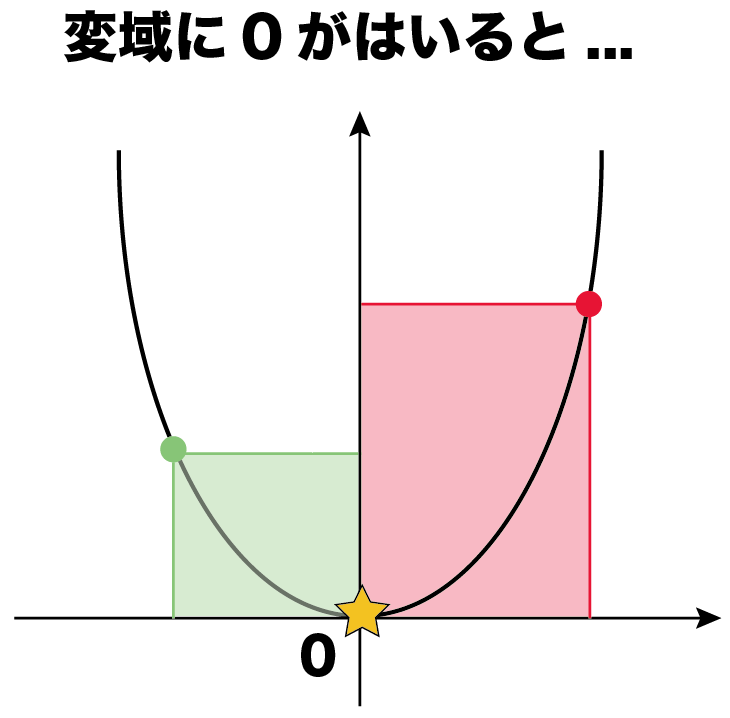 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 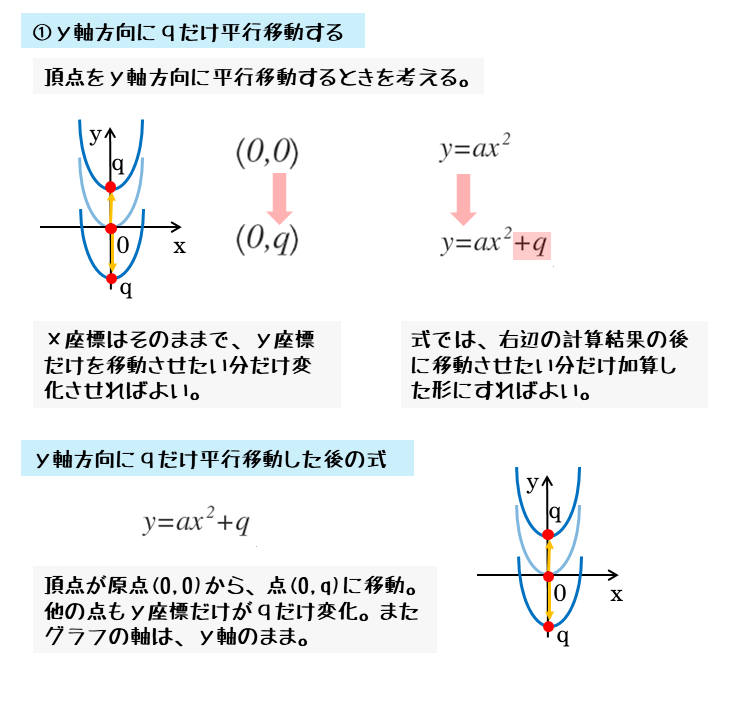 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ | 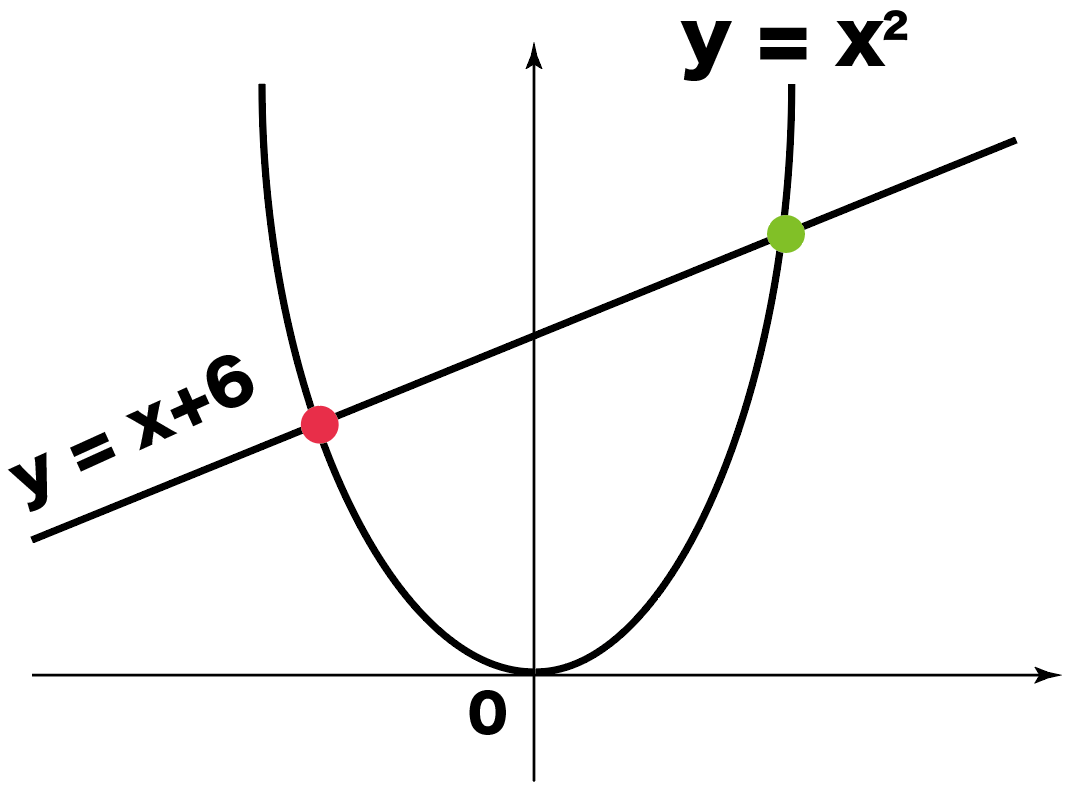 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
 関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |  関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ |
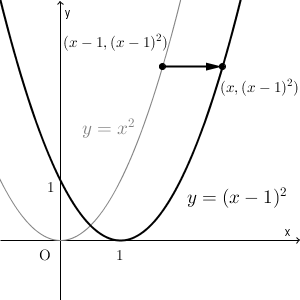
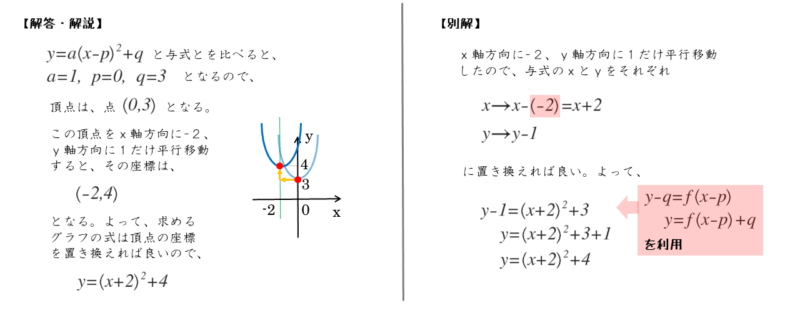
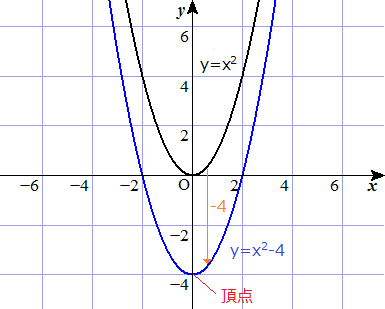
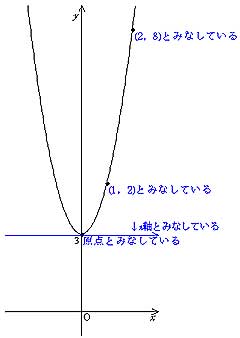
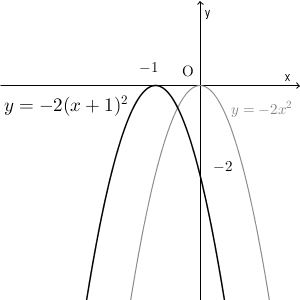
二次関数y=a (xp)^2のグラフ 例として、 y = x 2 のグラフを 軸方向に 1 だけ移動したものを考えてみます。 グラフは次のようになります。 グレーが移動前、黒い太線が移動後のグラフです。 各点の移動に注目して、グラフを見ながら点の座標をいくつか下図をみてください。2次関数のグラフを示しました。 2次関数の平行移動 原点を頂点とする2次関数y=ax 2 をx軸に2移動させました。グラフをある方向に一定の距離移動させることを「平行移動」といいます。 平行移動後の2次関数はx＝2のときy＝0です。
Incoming Term: 二次関数 y=x2乗 グラフ,
